Sucesiones numéricas
Una sucesión numérica se formaliza como una aplicación de los naturales en los reales, es decir :
que escribiremos simplemente como
o, si se da por entendido que los subíndices son enteros, también vale 
.
El nombre que recibe la sucesión también puede hacer referencia a los valores que toma sobre los reales, así, si la imagen de
fuesen los racionales, es decir fracciones enteras del tipo 
, podemos llamarla sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos, trascendentes, ... .
Notas y ejemplos básicos
Para definir término a término la sucesión, se indica para cada termino el valor que le corresponde directamente:
El primero es
a por ejemplo 3,
el segundo es
a por ejemplo -10,
el tercero es
a por ejemplo 9, y así sucesivamente.
Para indicar, si hace falta, el comportamiento del resto de los valores, se usa el término general y se escribe acompañado como
a por ejemplo número al azar, ... .
Los puntos suspensivos dan por entendido que los valores de la sucesión se omiten ya que estos quedan claramente determinados hasta el infinito, siendo el n-ésimo valor,
, el portador del método para generar el valor de cada término, y el nombre 
puede ser cambiado, si hace falta, por , i, j, k, ... .
Materialmente seria: 3, -10, 9, 7, ... , número al azar, ... .
Sucesión finita
Diremos que una sucesión es finita si determinamos su último termino, por ejemplo el n-ésimo:
Genéricamente:
, donde 
sería el término general si hiciese falta.
ejemplo: 100, 99, 98, ... , 1, 0.
Sucesión constante
Diremos que una sucesión es constante si todos los términos valen a , un número real cualquiera, ejemplo:
Genéricamente
.
ejemplo: si
queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1.
Sucesión creciente
Si imponemos al termino general, de una sucesión numérica, la condición que
, es decir, que el siguiente término, 
, siempre sea mayor estricto que su predecesor, 
, se llaman sucesiones estrictamente crecientes:
Para naturales: 1, 2, 3, 4, 5, 6, ... .
Para enteros: -10, -9, -8, -7, -6, ... .
Para reales:
.
Si imponemos
, es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes.
Sucesión decreciente
Al igual que las crecientes tenemos, según el termino general, que:
Si
entonces la sucesión es decreciente,
si
es estrictamente decreciente.
Sucesión alternada
Intuitivamente se llama sucesión alternada cuando alterna valores de signo opuesto, como an = ( − 1)n que nos genera la sucesión: 1, -1, 1, -1, 1, -1, ... . Utilizado por las series llamadas series alternas.
Según el término general
El termino general de la sucesión queda definido de forma explícita si su valor está en función del valor del subíndice, es decir, si
donde 
es una función cualquiera como por ejemplos:
que daría la sucesión de naturales sucesivos, es decir, 1, 2, 3, 4, 5, ... .
que daría todos los número pares incluido el cero, es decir, 0, 2, 4, 6, 8, ... .
que daría la sucesión de cuadrados siguiente, 0, 1, 4, 9, 16, ... .
Dada una función
, llamaremos extensión en los reales de 
a una función 
cuyos valores coinciden en el dominio de , es decir, 
.
Error fatal es nombrar a la extensión en los reales con el mismo nombre ¡
!, pues, se trata de una asociación totalmente arbitraria y no univoca que trae confusión y no tiene sentido para algunas funciones definidas a trozos. Compruébese que 
solo si la sucesión que determinan sobre los enteros es la misma, pero ¡no son la misma función!, llamemos a la extendida por ejemplo o 
si es un polinomio, o g o h si son funciones trigonométricas, agregando subíndices si hace falta.
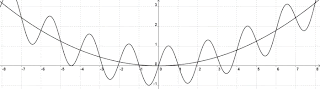
La función f puede adquirir propiedades de la extendida P, si existe P con dichas propiedades, como límites al infinito, monotonía, acotaciones... .
Casos en los que f no puede extenderse sobre los reales:
si definimos un como el número de factores propios de n.
funciones aritméticas, como la función fi de Euler o la Función de Möbius µ.
El término general de la sucesión queda definido de forma implícita si su valor depende de sus predecesores, esto se indica en general del modo siguiente:
Dados previamente los valores de
, podemos definir el término general de forma inductiva como 
como por ejemplo con la ecuación en diferencias 
Una sucesión numérica se formaliza como una aplicación de los naturales en los reales, es decir :
que escribiremos simplemente como
o, si se da por entendido que los subíndices son enteros, también vale 
.El nombre que recibe la sucesión también puede hacer referencia a los valores que toma sobre los reales, así, si la imagen de
fuesen los racionales, es decir fracciones enteras del tipo 
, podemos llamarla sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos, trascendentes, ... .Notas y ejemplos básicos
Para definir término a término la sucesión, se indica para cada termino el valor que le corresponde directamente:
El primero es
a por ejemplo 3,el segundo es
a por ejemplo -10,el tercero es
a por ejemplo 9, y así sucesivamente.Para indicar, si hace falta, el comportamiento del resto de los valores, se usa el término general y se escribe acompañado como
a por ejemplo número al azar, ... .Los puntos suspensivos dan por entendido que los valores de la sucesión se omiten ya que estos quedan claramente determinados hasta el infinito, siendo el n-ésimo valor,
, el portador del método para generar el valor de cada término, y el nombre 
puede ser cambiado, si hace falta, por , i, j, k, ... .Materialmente seria: 3, -10, 9, 7, ... , número al azar, ... .
Sucesión finita
Diremos que una sucesión es finita si determinamos su último termino, por ejemplo el n-ésimo:
Genéricamente:
, donde 
sería el término general si hiciese falta.ejemplo: 100, 99, 98, ... , 1, 0.
Sucesión constante
Diremos que una sucesión es constante si todos los términos valen a , un número real cualquiera, ejemplo:
Genéricamente
.ejemplo: si
queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1.Sucesión creciente
Si imponemos al termino general, de una sucesión numérica, la condición que
, es decir, que el siguiente término, 
, siempre sea mayor estricto que su predecesor, 
, se llaman sucesiones estrictamente crecientes:Para naturales: 1, 2, 3, 4, 5, 6, ... .
Para enteros: -10, -9, -8, -7, -6, ... .
Para reales:
.Si imponemos
, es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes.Sucesión decreciente
Al igual que las crecientes tenemos, según el termino general, que:
Si
entonces la sucesión es decreciente,si
es estrictamente decreciente.Sucesión alternada
Intuitivamente se llama sucesión alternada cuando alterna valores de signo opuesto, como an = ( − 1)n que nos genera la sucesión: 1, -1, 1, -1, 1, -1, ... . Utilizado por las series llamadas series alternas.
Según el término general
El termino general de la sucesión queda definido de forma explícita si su valor está en función del valor del subíndice, es decir, si
donde 
es una función cualquiera como por ejemplos:
que daría la sucesión de naturales sucesivos, es decir, 1, 2, 3, 4, 5, ... .
que daría todos los número pares incluido el cero, es decir, 0, 2, 4, 6, 8, ... .
que daría la sucesión de cuadrados siguiente, 0, 1, 4, 9, 16, ... .Dada una función
, llamaremos extensión en los reales de 
a una función 
cuyos valores coinciden en el dominio de , es decir, 
.Error fatal es nombrar a la extensión en los reales con el mismo nombre ¡
!, pues, se trata de una asociación totalmente arbitraria y no univoca que trae confusión y no tiene sentido para algunas funciones definidas a trozos. Compruébese que 
solo si la sucesión que determinan sobre los enteros es la misma, pero ¡no son la misma función!, llamemos a la extendida por ejemplo o 
si es un polinomio, o g o h si son funciones trigonométricas, agregando subíndices si hace falta.
La función f puede adquirir propiedades de la extendida P, si existe P con dichas propiedades, como límites al infinito, monotonía, acotaciones... .
Casos en los que f no puede extenderse sobre los reales:
si definimos un como el número de factores propios de n.
funciones aritméticas, como la función fi de Euler o la Función de Möbius µ.
El término general de la sucesión queda definido de forma implícita si su valor depende de sus predecesores, esto se indica en general del modo siguiente:
Dados previamente los valores de
, podemos definir el término general de forma inductiva como 
como por ejemplo con la ecuación en diferencias 
