Tercer periodo (sucesiones aritméticas)

Definición de sucesión aritmética

Una sucesión 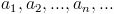es una sucesión aritmética si hay un número real d tal que para todo entero positivo k.
.

El número se le llama diferencial común de la sucesión.
Dada una sucesion aritmetica:k+1 = a+ d

Para todo entero positivo K. Esto nos da una formula recursiva para encontrar terminos sucesivos .A partir de cualquier numero real a1. obtendremos una sucesion aritmetica con diferencia comun d con solo agregar d a a1, luego a a1+d y asi sucesivamente, con lo que resulta observa que la diferencia común d es la diferencia de dos términos sucesivos cualesquiera de una sucesión aritmética.

El n-ésimo término de una sucesión aritmética


Teorema: fórmulas para

Si es una sucesión aritmética con diferencia común d, entonces la n-ésima suma parcial (esto es, la suma de los primeros términos), está dada por       o     

Demostración
Podemos escribir

.

Con el uso repetido de las propiedades conmutativa y asociativa de números reales resulta
.


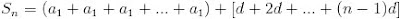con veces dentro del primer par de paréntesis. Así .

La expresión dentro de corchetes es la suma de los primeros enteros positivos. Con la fórmula para la suma de los primeros n enteros positivos, , entonces tenemos
 


Sustituimos en la última ecuación por y factorizamos con lo cual
 


Puesto que , la última ecuación es equivalente a
 .